Radix
| Numeral systems by culture | |
|---|---|
| Hindu-Arabic numerals | |
| Western Arabic (Hindu numerals) Eastern Arabic Indian family Tamil |
Burmese Khmer Lao Mongolian Thai |
| East Asian numerals | |
| Chinese Japanese Suzhou |
Korean Vietnamese Counting rods |
| Alphabetic numerals | |
| Abjad Armenian Āryabhaṭa Cyrillic |
Ge'ez Greek Georgian Hebrew |
| Other systems | |
| Aegean Attic Babylonian Brahmi Egyptian Etruscan Inuit |
Kharosthi Mayan Quipu Roman Sumerian Urnfield |
| List of numeral system topics | |
| Positional systems by base | |
| Decimal (10) | |
| 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 15, 16, 20, 24, 30, 36, 60, 64 | |
| Non-positional system | |
| Unary numeral system (Base 1) | |
| List of numeral systems | |
In mathematical numeral systems, the base or radix for the simplest case is the number of unique digits, including zero, that a positional numeral system uses to represent numbers. For example, for the decimal system (the most common system in use today) the radix is ten, because it uses the ten digits from 0 through 9.
In any numeral system, the base is written as "10". In a base ten numeral system, "10" represents the number ten; in a base two system, "10" represents the number two.
Contents |
Etymology
Radix is a Latin word for "root". Root can be considered a synonym for base in the arithmetical sense.
In numeral systems
In the system with radix 13, for example, a string of digits such as 398 denotes the decimal number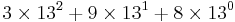 
. More generally, in a system with radix b (b > 1), a string of digits 
denotes the decimal number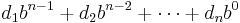 
.
Commonly used numeral systems include:
- The decimal system, the most used system of numbers in the world, is used in arithmetic. Its ten digits are "0–9".
- The duodecimal (dozenal) system, which is base 12, is often used due to divisibility by 2, 3, 4 and 6. It was traditionally used as part of quantities expressed in dozens and grosses.
- The binary numeral system, used internally by nearly all computers, is base two. The two digits are "0" and "1", expressed by different electric charges.
- The hexadecimal system, which is base 16, is often used in computing. The sixteen digits are "0–9" followed by "A–F".
- The octal system, which is base 8, is occasionally used in computing. The eight digits are "0–7".
- Base 64 is also occasionally used in computing, using as digits "A–Z", "a–z", "0–9", plus two more characters, often "+" and "/".
The octal, hexadecimal and base-64 systems are often used in computing because of their ease as shorthand for binary. For example, every hexadecimal digit has an equivalent 4 digit binary number.
Radices are usually natural numbers. However, more sophisticated positional systems are possible, e.g. golden ratio base (whose radix is a non-integer algebraic number), and negative base (whose radix is negative).
In exponentiation
In exponentiation, the base refers to the number b in an expression of the form bn. The number n is called the exponent and the expression is known formally as exponentiation of b by n or the exponential of n with base b. It is more commonly expressed as "the nth power of b", "b to the nth power" or "b to the power n".
When the nth power of b equals a number a, or a = bn , then b is called an "nth root" of a. The term power strictly refers to the entire expression, but is sometimes used to refer to the exponent.
The inverse function to exponentiation with base b (when it is well-defined) is called the logarithm to base b, denoted logb. Thus:
